基础

Lingo语句以 ; 结束 包括注释！！！！

Lingo解最大最小值的问题一般将式子放在最上面，下面是约束条件和初值条件，见案例1

sets：
!学生集：性别属性sex，1表示男性，0表示女性；年龄属性age.  ;
students/John,Jill,Rose,Mike/:sex,age;
!男学生和女学生的联系集：友好程度属性friend，[0，1]之间的数。;
linkmf(students,students)|sex(&1) #eq# 1 #and# sex(&2) #eq# 0: friend;
!男学生和女学生的友好程度大于0.5的集;
linkmf2(linkmf) | friend(&1,&2) #ge# 0.5 : x;
endsets

data:
sex,age = 1 16
	0 14
	0 17
	0 13;
friend = 0.3 0.5 0.6;
enddata

用竖线（|）来标记过滤器的开始，&1可看作派生集的第1个原始父集的索引，它取遍该原始父集的所有成员。

符号总结

@符号

@gin(x) 规定x为非负整数

@bin(x) 规定x为0或1，是对题目的约束进行简化的有效函数

@abs(x) 返回x的绝对值

@sin(x) 返回x的正弦值，x采用弧度制

@cos(x) 返回x的余弦值

@tan(x) 返回x的正切值

@exp(x) 返回常数e的x次方

@log(x) 返回x的自然对数

@lgm(x) 返回x的gamma函数的自然对数

@sign(x) 如果x<0返回-1；否则，返回1

@floor(x) 返回x的整数部分。当x>=0时，返回不超过x的最大整数；当x<0时，返回不低于x的最大整数。

@smax(x1,x2,…,xn) 返回x1，x2，…，xn中的最大值

@smin(x1,x2,…,xn) 返回x1，x2，…，xn中的最小值

#逻辑符号

LINGO具有９种逻辑运算符：

#not# 否定该操作数的逻辑值，＃not＃是一个一元运算符

#eq# 若两个运算数相等，则为true；否则为flase

#ne# 若两个运算符不相等，则为true；否则为flase

#gt# 若左边的运算符严格大于右边的运算符，则为true；否则为flase

#ge# 若左边的运算符大于或等于右边的运算符，则为true；否则为flase

#lt# 若左边的运算符严格小于右边的运算符，则为true；否则为flase

#le# 若左边的运算符小于或等于右边的运算符，则为true；否则为flase

#and# 仅当两个参数都为true时，结果为true；否则为flase

#or# 仅当两个参数都为false时，结果为false；否则为true

这些运算符的优先级由高到低为：

高 #not#

#eq# #ne# #gt# #ge# #lt# #le#

低 #and# #or#

案例

案例1

model:
	min=8*x11+6*x12+10*x13+9*x21+12*x22+7*x23+7*x31+4*x32+3*x33;

	x11+x21+x31=1;
	x12+x22+x32=1;
	x13+x23+x33=1;
    
	x11+x12+x13=1;
	x21+x22+x23=1;
	x31+x32+x33=1;
    
	!@bin(9);
	@bin(x11);@bin(x12);@bin(x13);
	@bin(x21);@bin(x22);@bin(x23);
	@bin(x31);@bin(x32);@bin(x33);
end

案例2 常见线性规划模型

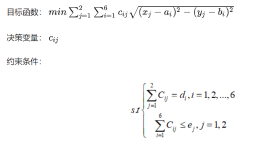
已知参数：

a=1.25， 8.75 ，0.5， 5.75 ，3 ，7.25

b=1.25， 0.75 ，4.75 ，5，6.5， 7.75

d=3 ，5 ，4， 7， 6 ，11

e=20， 20

x=5， 2

y=1， 7

解:

model:

! 集合的用法;
sets:
S/1..6/: a,b,d ;
T/1..2/: e,x,y ;
U(S,T): c ;
endsets

data:
a=1.25 8.75 0.5 5.75 3 7.25;
b=1.25 0.75 4.75 5 6.5 7.75;
d=3 5 4 7 6 11;
e=20 20;
x=5 2;
y=1 7;
enddata

! 这里是式子;
min= @sum(T(j):@sum(S(i):
	c(i,j)*@sqrt(( x(j) -a(i) )^2 + ( y(j) - b(i) )^2 ) 
	));

! 这里是约束条件;
@for(S(i):
	@sum(T(j): c(i,j))=d(i)
	);
@for(T(j):
	@sum(S(i): c(i,j))<= e(j)
	);

end